Boosting이란?

m1~m3 모델이 있을 때 m1에서는 x에서 샘플링된 데이터를 넣는다.
m1에서 나온 결과 중 예측이 잘못된 값들에 가중치를 반영해서 다음 모델인 m2에 넣는다.
(올바르게 예측한 샘플에 대해서는 가중치를 감소시킨다)
마찬가지로 y2 결과에서 예측이 잘못된 값들에 가중치를 반영해서 m3에 넣는다.
각 모델 성능이 다르므로 각 모델에 가중치 W를 반영한다.
>> 새로운 모델이 추가될 때마다 오류 최소화를 목표로 학습되고, 실제 값과 예측 값 사이의 오류가 줄어들게 된다.
Boosting을 사용하는 대표적인 모델은 Adaboost, Gradient Boosting 등이 있고, XGBoost는 그 중 gradient를 이용하여 boosting하는 gradient boosting을 사용해서 모델링을 한다.
Gradient boosting을 알려면 adaboost를,
adaboost를 알려면 random forest를,
random forest를 알려면 decision tree를 알아야 한다.
순서대로 알아보자.
Decision Tree

데이터를 가장 잘 구분할 수 있는 질문을 기준으로 나눈다.
지나치게 많이 구분하면 오버피팅이 되므로 이를 막기 위해 가지치기(pruning)를 한다.
최대 깊이 / 터미널 노드의 최대 개수 / 한 노드가 분할하기 위한 최소 데이터 수를 제한한다.
어떤 트리가 좋은 트리일까?에 대한 기준

entropy = 불순도를 수치로 나타낸 것. 0 = 최소, 1 = 최대
information gain = entropy(parent) - [weighted average]entropy(children)
>> entropy(parent) = 분기 이전 엔트로피 / entropy(children) = 분기 이후 엔트로피
Decision tree는 information gain을 최대화하는 방향으로 학습이 진행된다.
어느 feature의 어느 분기점에서 정보 획득이 최대화되는지 판단을해서 분기가 진행된다.
장점)
- inference time이 빠르다
- interpretable
단점)
- 큰 나무는 overfitting이 잘된다
- low level에서 data가 매우 부족
Random Forest
Decision tree가 모여 random forest를 구성한다.

Feature이 N개 있을 때 그 중 랜덤하게 n개만 선택해서 decision tree를 만들고,
또 N개 중 랜덤하게 n개만 선택해서 또다른 decision tree를 만들고.. 이를 반복하여 여러 개의 decision tree를 만든다.
각 decision tree의 예측값들 중 가장 많이 나온 값을 최종 예측값으로 (hard voting) 정한다.
각각의 decision tree는 동등한 가중치를 가지고 있다.
즉, 하나의 거대하고 overfitting된 decision tree를 만들기보다 여러 개의 작은 decision tree를 만드는 것.
AdaBoost

AdaBoost는 여러 개의 stump로 구성되어 있다.

stump는 단 하나의 질문으로 데이터를 분류해야하므로 정확한 분류를 못한다. 즉, weak learner이다.
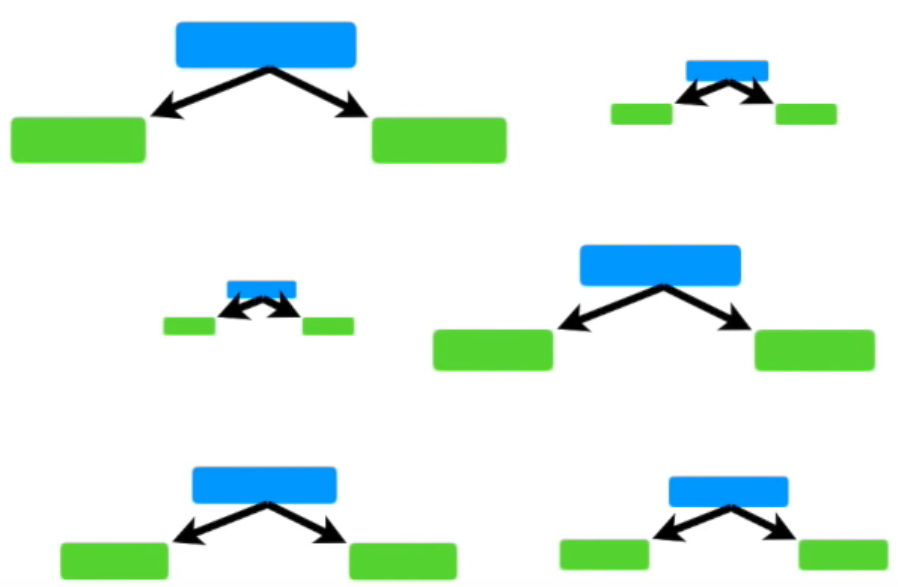
AdaBoost에서는 특정 stump의 가중치가 더 높다.

AdaBoost에서는 가중치가 높다는 것을 Amount of Say가 높다고 표현한다.
첫번째 stump에서 발생한 에러는 두번째 stump의 결과에,
두번째 stump에서 발생한 에러는 세번째 stump의 결과에 ... 마지막 stump까지 영향을 준다.
example)
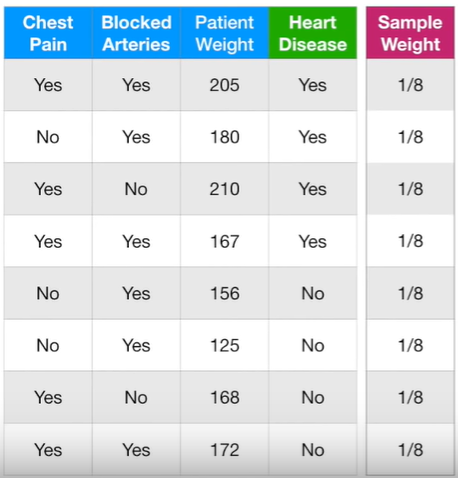
각 feature가 target value = heart disease에 미치는 영향에 대해 AdaBoost 방식으로 알아보자.

chest pain이 yes일 때 heart disease도 yes인 것 3 (correct)
chest pain이 yes일 때 heart disease는 no인 것 2 (incorrect)
chest pain이 no일 때 heart disease도 no인 것 2 (correct)
chest pain이 no일 때 heart disease는 yes인 것 1 (incorrect)
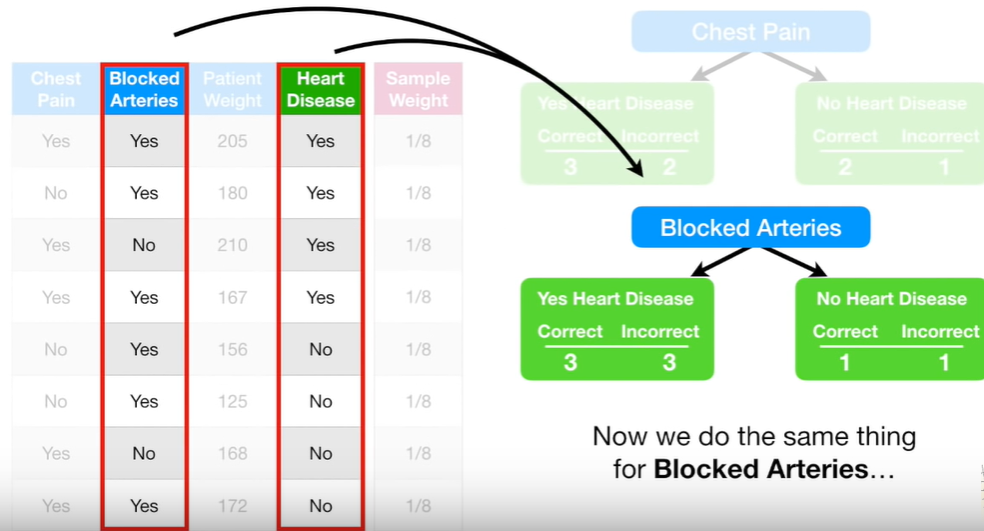
같은 방법으로 blocked arteries에 대해서 분류

1) 몸무게를 오름차순으로 정렬한 뒤,
2) 인접한 몸무게의 평균을 구한 다음, (ex. 205 -- 192.5 -- 180)
3) 각 평균 값마다 지니 불순도를 계산
4) 가장 작은 지니 불순도를 갖는 인접 몸무게 평균값을 분기 기준으로 잡음 = 176
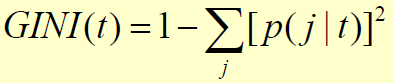
지니 계수는 어떤 샘플을 뽑았을 때 그 샘플이 잘못 분류될 확률을 의미한다.
그러므로 지니 계수가 0에 가까울수록 잘못 분류될 확률이 적은 것.
위 표에서 지니 계수 = 1 - (prob of 'yes')^2 - (prob of 'no')^2
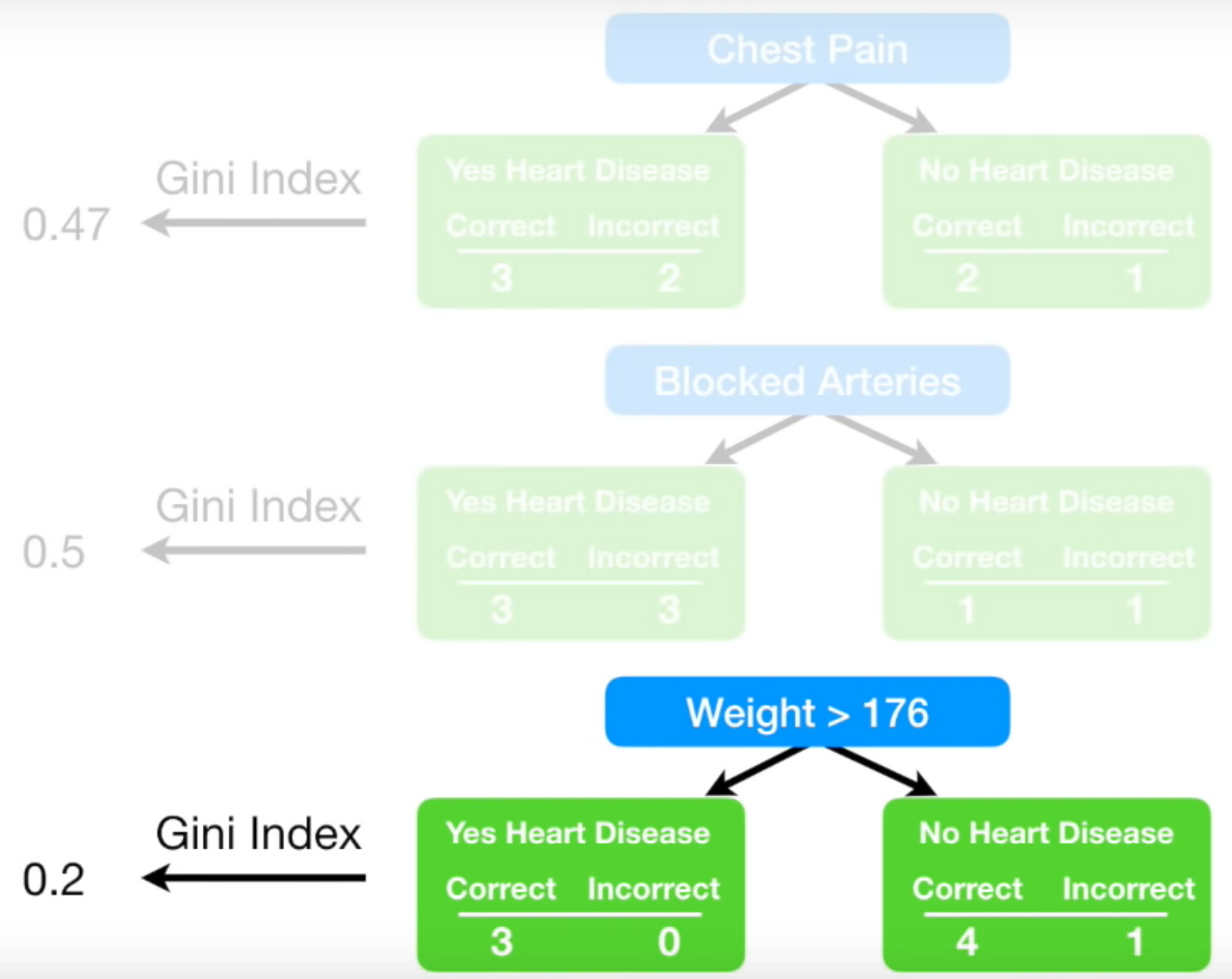
이렇게 각 stump에 대해서 계산한 다음에 각 stump의 지니 계수를 계산한다.
마지막 stump의 지니 계수가 가장 작기 때문에 마지막 stump를 forest의 첫 stump로 지정한다.
이 stump가 최종 결과 예측에 얼만큼 중요한지 알아보자.
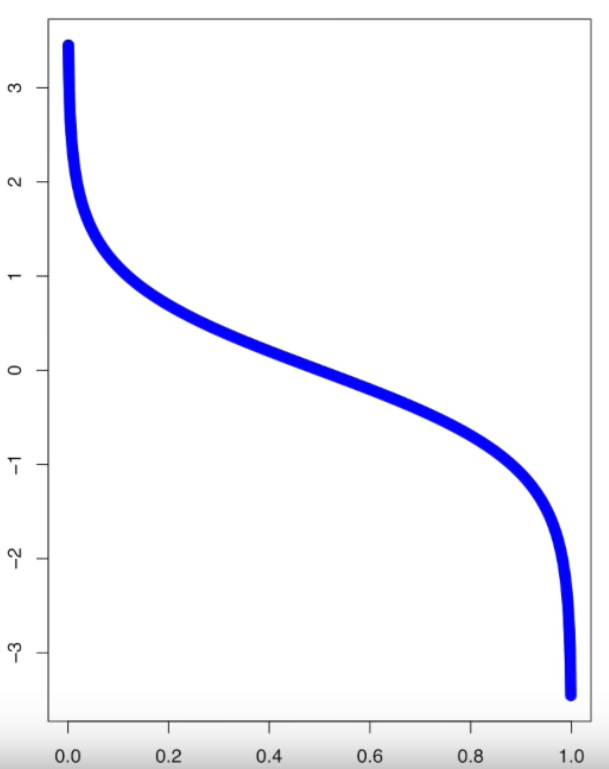
X축은 total error, Y축은 Amount of Say.
total error = 0 이면 항상 올바른 분류를 한다는 뜻이고, 1이면 항상 반대로 분류를 한다는 뜻이다.
total error = 0.5일 때는 amount of say가 0이다.
위 stump에서 incorrect는 총 8개 중 1개이므로 total error = 1/8
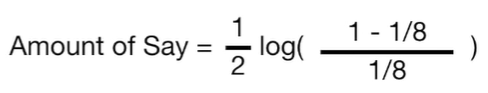
= 0.97

하나의 stump가 잘못 분류한 sample에 대해서 다음 stump로 넘겨줄 때 가중치를 더 높여서 넘겨준다.
맨 처음 stump에서 빨간 네모 sample을 잘못 분류했으므로 해당 sample의 weight를 1/8보다 크게하고, 나머지 sample의 weight는 1/8보다 작게 해서 다음 stump로 넘겨준다.
new sample weight = (1/8) x e ^ 0.97 = (1/8) x 2.64 = 0.33
기존의 weight = 1/8 = 0.125보다 높아졌다.

잘 분류한 sample들의 weight들을 계산하려면 amount of say에 -부호만 붙이면 된다.
new sample weight = (1/8) x e ^ (-0.97) = (1/8) x 0.38 = 0.05
기존의 weight = 1/8 = 0.125보다 작아졌다.
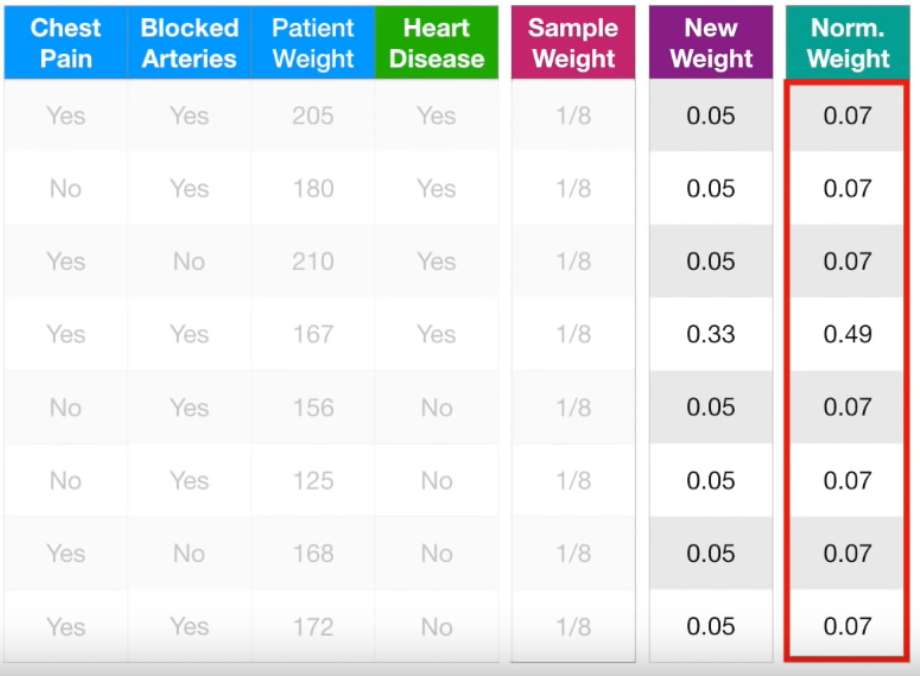
new sample weight를 update하고, 다 더했을 때 1이 되도록 normalize해준다.
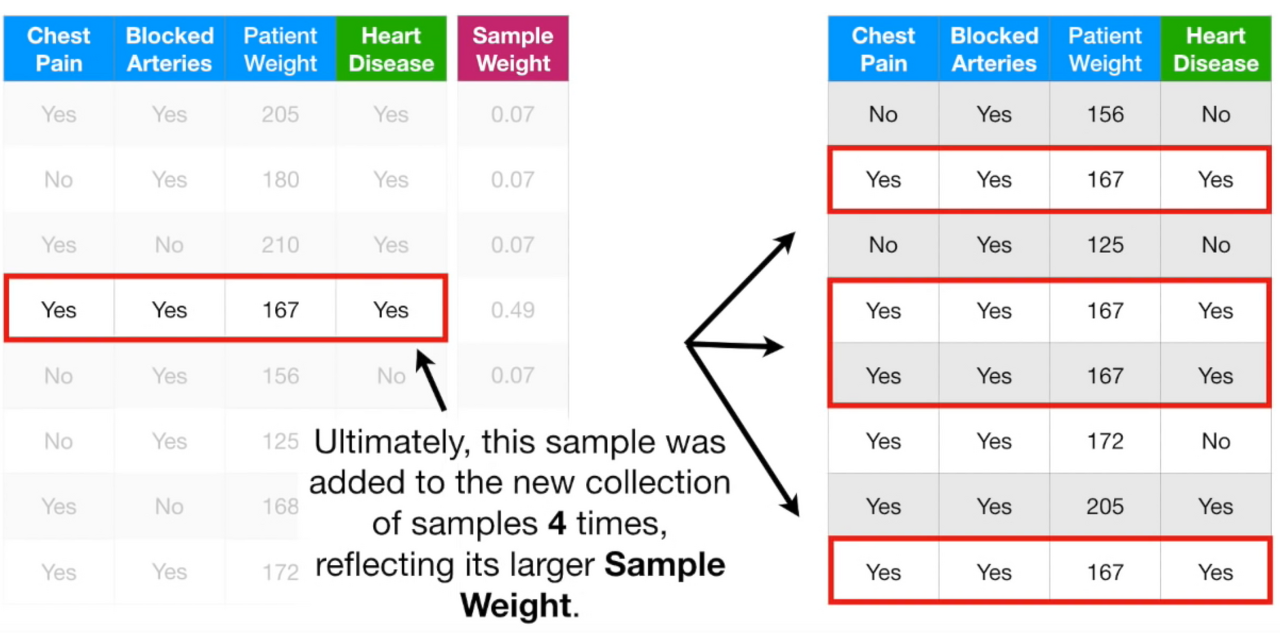
테이블을 샘플링한다.
0~1 사이 숫자를 무작위로 뽑아서 범위에 따라서 i번째 샘플을 선택한다.
ex. 0~0.07 / 0.07~0.14 / 0.14~0.21 / 0.21~0.70 / 0.70~0.77 / ... >> weight값에 따라 범위가 다르다
범위가 큰 네번째 샘플이 뽑힐 확률이 크므로 중복적으로 뽑힌 것을 확인할 수 있다.
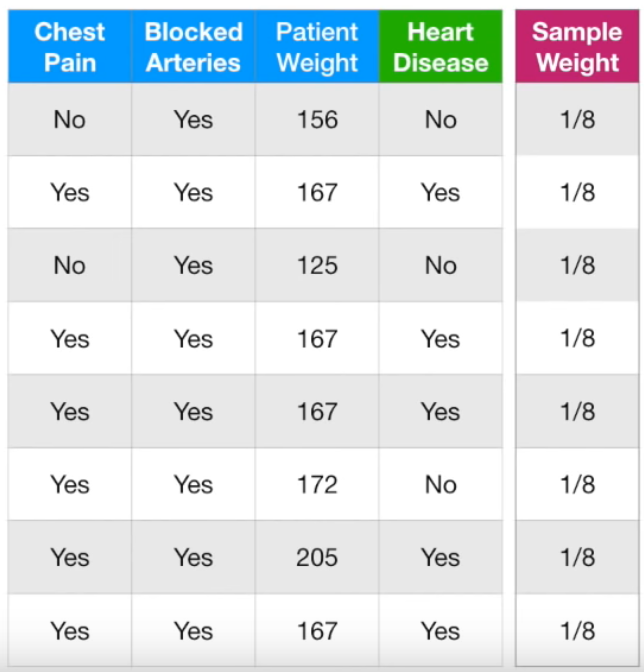
샘플링한 테이블에, sample weight을 다시 1/8으로 통일한다.
중복된 데이터는 4개가 있으므로 4/8의 weight을 가지는 것과 동일한 효과를 갖는다.
이는 처음에 잘못 분류를 했기 때문에 weight를 높여서 제대로 분류하기 위함이다.
weight가 높아졌으므로 해당 sample에 가중치를 더 두고 분류를 할 것이다.
다시 처음으로 돌아가서 진행한다.
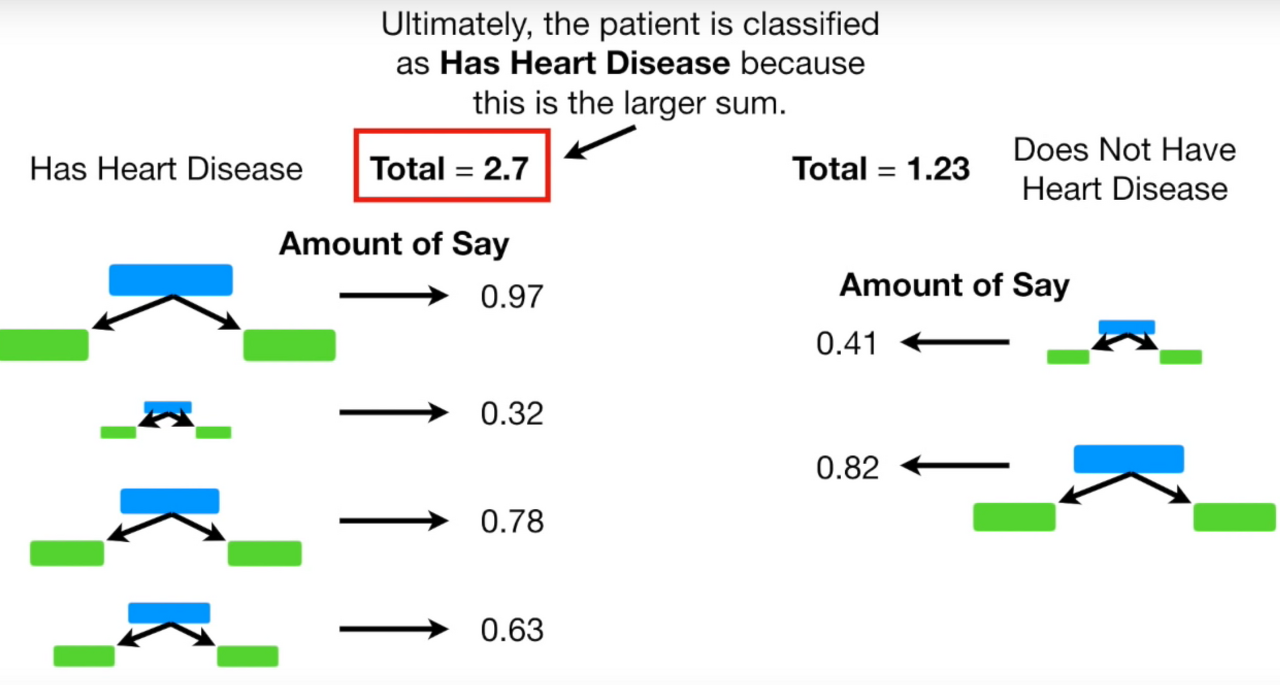
위는 AdaBoost를 여러 차례 진행한 결과.
왼쪽은 heart disease가 있다고 판단한 stump, 오른쪽은 없다고 판단한 stump.
각 stump의 amount of say를 더해서 total amount of say를 계산할 수 있는데, 왼쪽이 더 큰 것을 확인할 수 있다.
따라서 최종적으로 heart disease가 있다고 분류를 할 수 있다.
Gradient Boosting
AdaBoost는 하나의 stump에서 발생한 error가 다음 stump에 순차적으로 영향을 주어 최종 결과를 도출한다.
반면, Gradient boosting는 single leaf에서 시작하고, leaf가 8~32개로 구성된 tree로 구성되어 있다.
Leaf는 타겟 값에 대한 초기 추정 값을 나타내는데, 보통은 평균으로 정한다.
그 다음은 AdaBoost와 동일하게 이전 tree의 error는 다음 tree에 영향을 준다.
example)
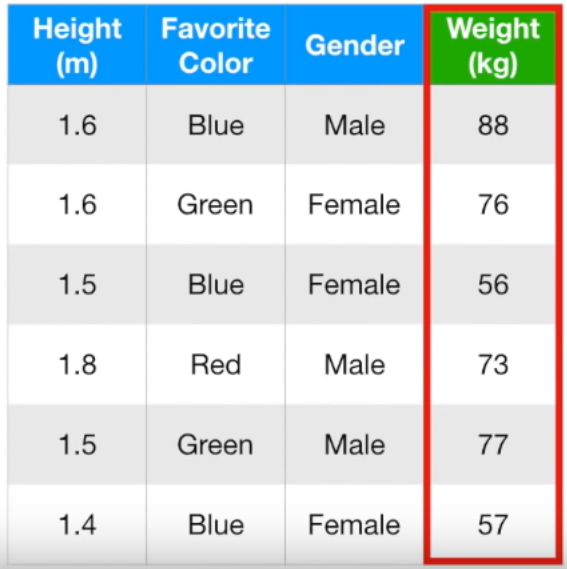
키, 좋아하는 색, 성별로 몸무게를 예측하는 Gradient Boost 모델을 만들어보자.
Single leaf는 타겟의 평균이므로 (88 + 76 + 56 + 73 + 77 + 57) / 6 = 71.2이다.
이제 single leaf에서 예측한 값과 실제 값의 차이 (=pseudo residual)를 반영한 새로운 트리를 만들어야 한다.
모든 행의 pseudo residual을 정리하면 다음과 같다.
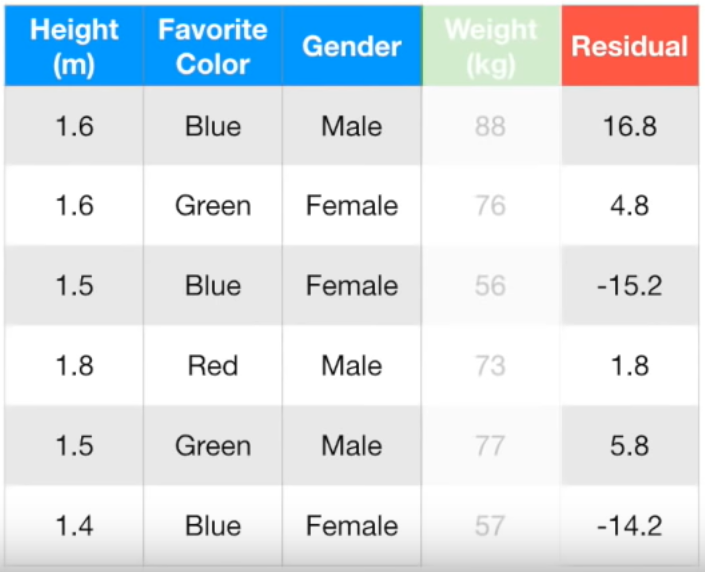
이제 실제 몸무게가 아니라 residual을 맞춰야한다.
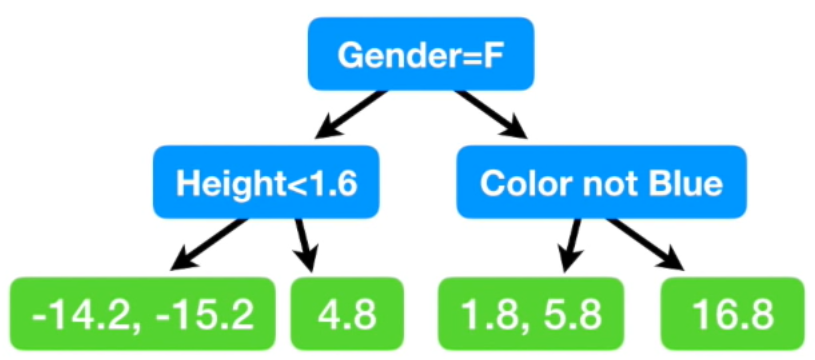
위와 같이 모델을 만들었다.
여자면 왼쪽, 남자면 오른쪽 / 1.6 미만이면 왼쪽, 이상이면 오른쪽 / 파란색이 아니면 왼쪽, 파란색이면 오른
그런데 두 개의 residual 값이 있는 경우가 있다. 그러면 두 값의 평균으로 치환해준다.
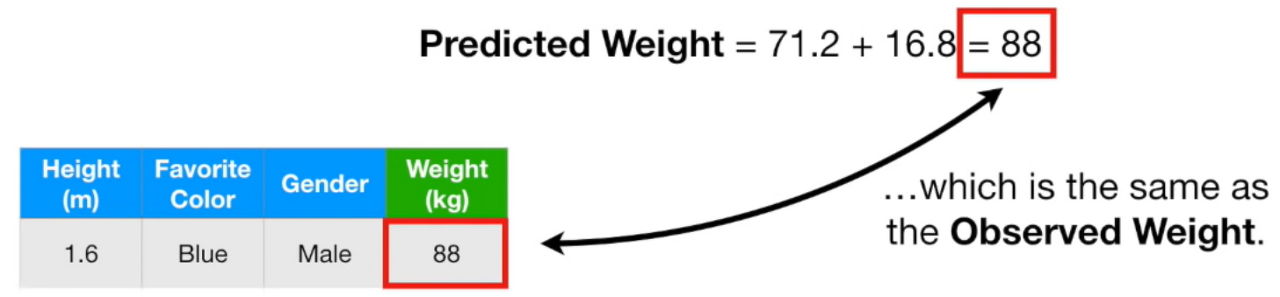
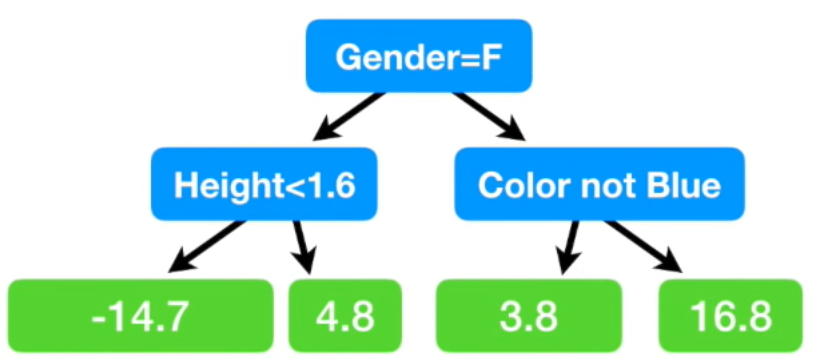
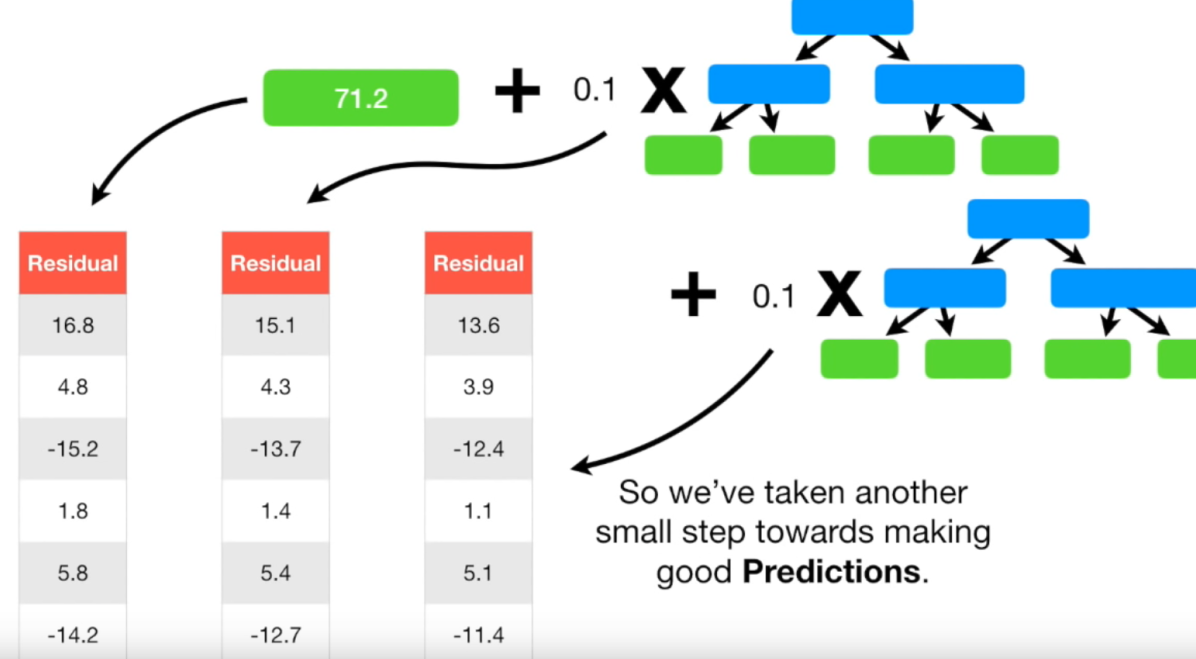
single leaf를 첫번째 트리라고 하고, 이후에 만든 트리를 두번째 트리라고 하자.
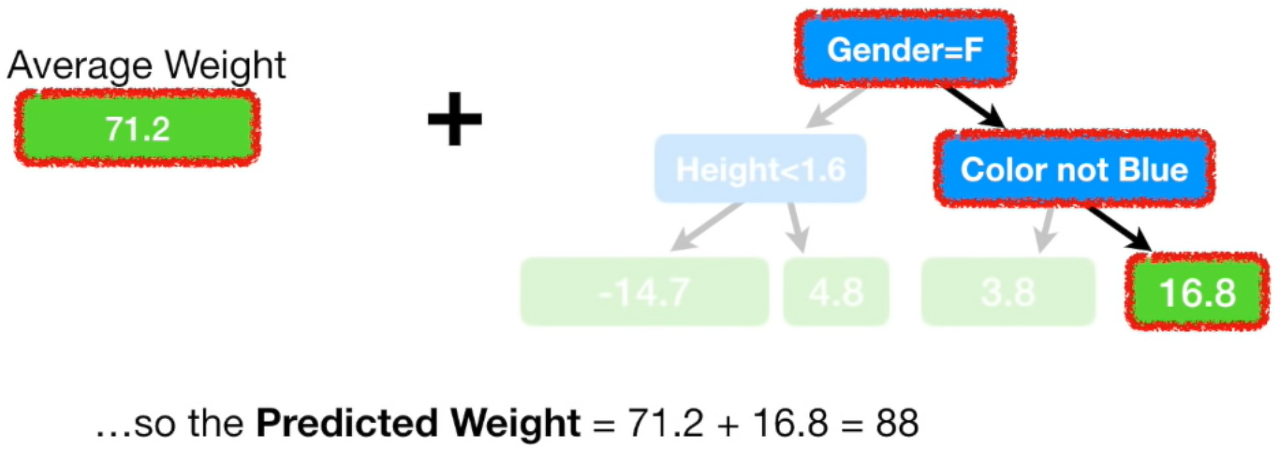
두번째 트리는 남자고, 파란색을 좋아하는 사람의 residual weight가 16.8이라고 예측했다.
이를 첫번째 트리와 더하게되면 88인데, 이 값은 실제 몸무게와 정확히 일치한다.
이는 훈련데이터에 overfitting되었다는 의미이다.
이를 조절하기 위해서 residual을 예측하는 모델(두번째모델)에 learning rate를 곱해준다.
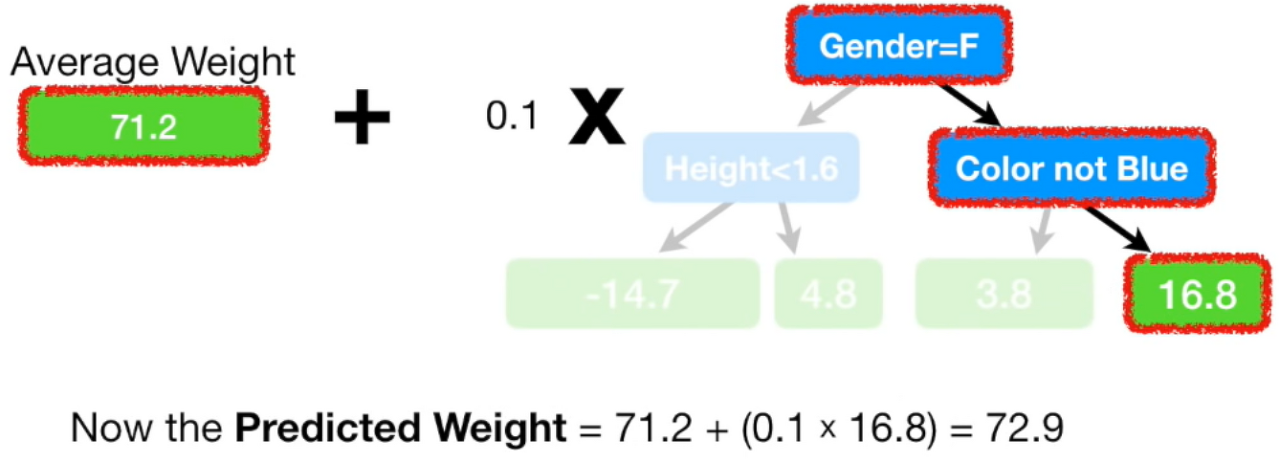
실제값 88보다는 멀어졌지만 첫 모델이 예측한 71.2보다는 88에 더 가까워진 것을 알 수 있다.
Gradient Boost 모델은 이런식으로 실제 값에 조금씩 가까워지는 방향으로 학습을 한다.
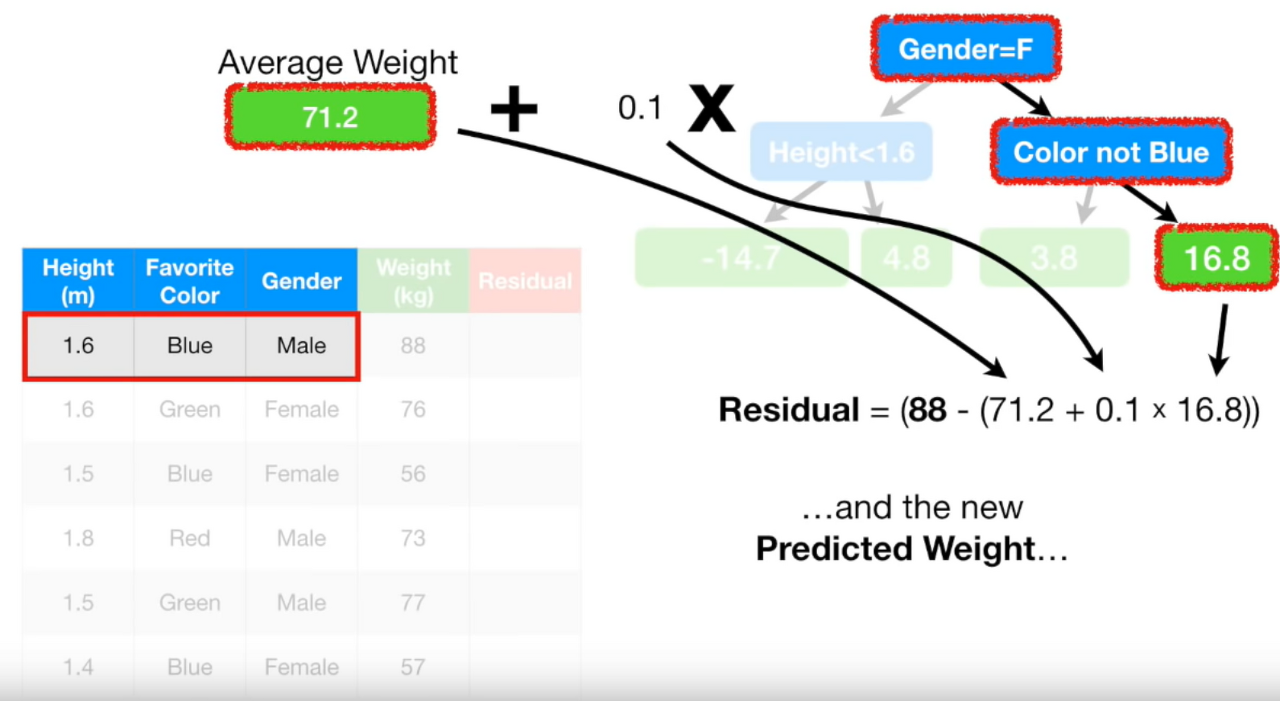
Pseudo residual을 다시 구해보자.
Pseudo residual = (실제값 - (예측값 + 학습률 * 이전 residual))
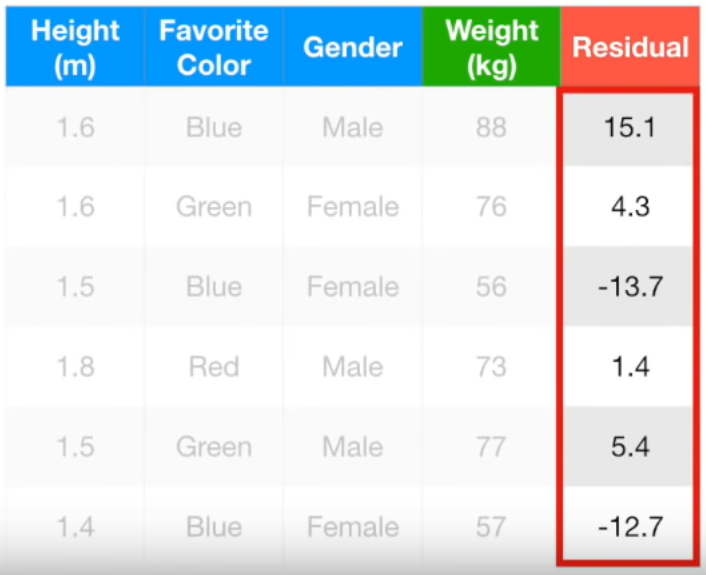
초기에 평균값으로만 구했던 residual보다 값이 작아졌다.
Residual이 작아졌다 = 실제 값과 예측 값의 차이가 작아졌다 = 조금씩 실제 값으로 다가가고 있다

세번째 트리까지 만들고난 뒤 남자이고 좋아하는 색이 파란색인 사람의 몸무게를 예측한 결과이다.
조금 더 88에 가까워지고 있다.
Iteration을 돌릴수록 residual도 조금씩 감소한다. 즉, 예측 정확도가 더 높아진다.
이 과정을 미리 정해둔 iteration 횟수에 도달하거나 더이상 residual이 작아지지 않을 때까지 반복한다.
XGBoost
Extreme Gradient Boosting의 약자이다. Gradient Boosting을 병렬적으로 실행한 것이다.
Regression과 classification 문제를 모두 지원한다.
장점)
- 병렬 처리로 학습, 분류 속도가 빠르다
- 과적합 규제 기능으로 강한 내구성을 지닌다
- 분류와 회귀 영역에서 뛰어난 예측 성능
- early stopping 기능이 있다
- customizing이 용이하다

학습과정은 Gradient Boosting과 비슷한데, 'calculate predicted probability' 단계가 추가되었다.
example)
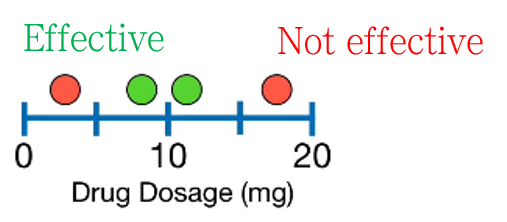
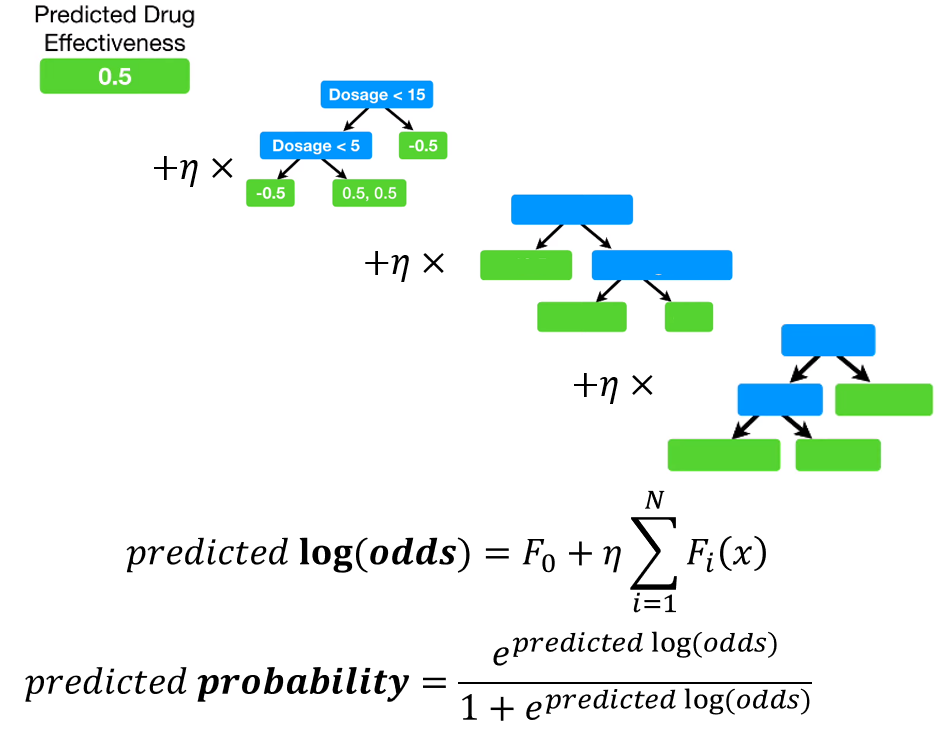
약 복용량에 따라서 약이 효과적일지 아닐지 구분하는 데이터이다. 이진 분류를 하려고 한다.
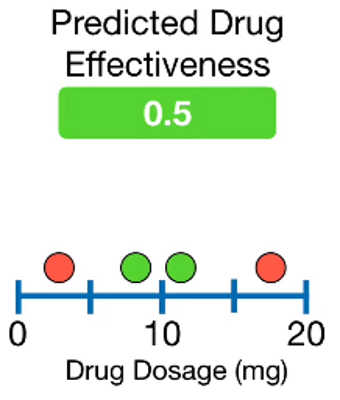
1. Single leaf(=첫번째모델)로 시작한다.
leaft의 값은 drug가 효과적일지 아닐지를 맞추는 확률값이다. Default값은 0.5이다.
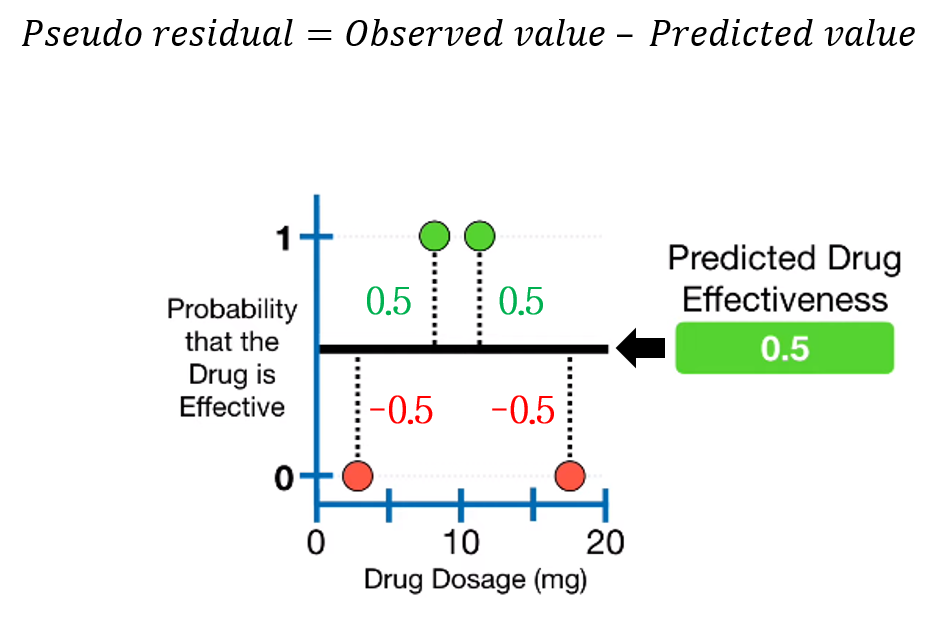
2. Pseudo residual을 계산한다.
3. 다음 트리를 만든다.
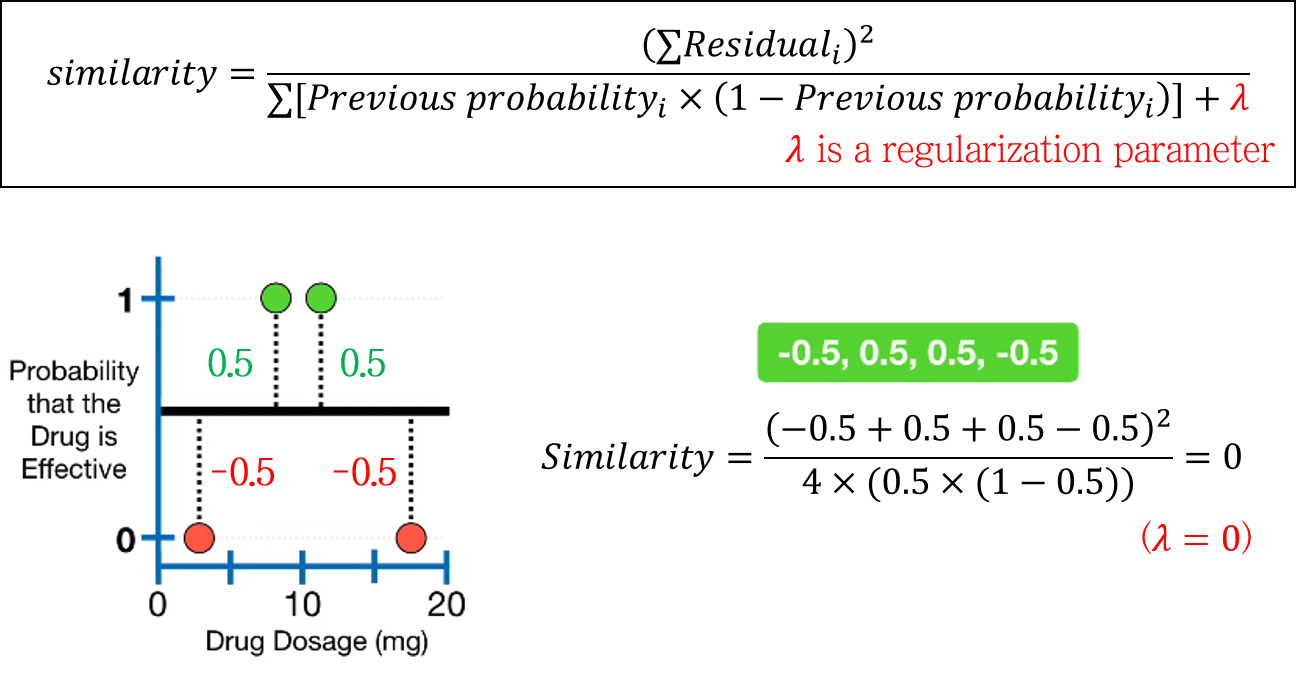
3-1. similarity score를 계산한다.
lambda는 regularization term으로 overfitting을 방지해준다.
모든 data point를 넣으면 similarity=0이 나온다.
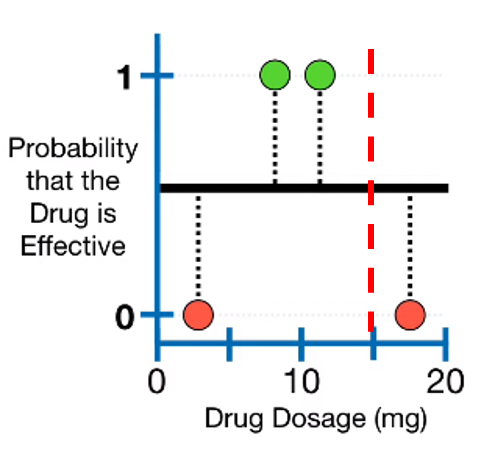
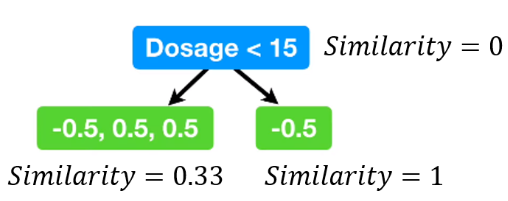
가장 오른쪽 두 point의 평균인 15를 기준점으로 잡아서 데이터를 나누고 similarity를 다시 계산하면 위와 같다.
3-2. Gain을 계산한다.
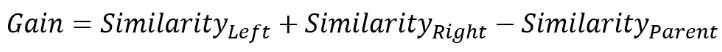
Gain이 가장 큰 조건(이 예제에서는 dosage)이 분기 조건이 된다.
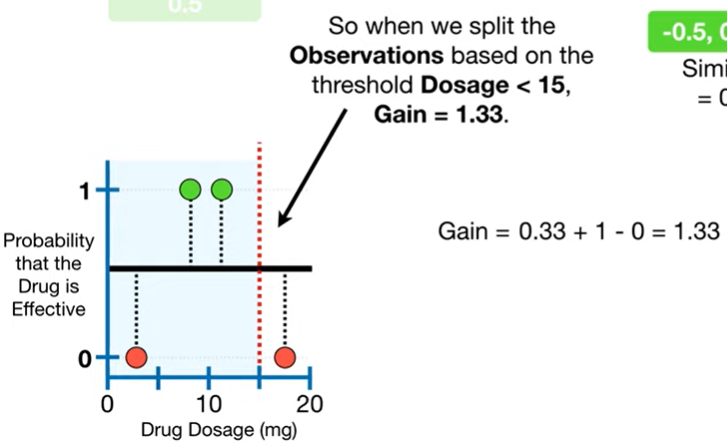
Dosage < 15 일 때의 gain = 0.33 + 1 - 0 = 1.33이고, 이 때의 gain이 다른 조건들과 비교했을 때 가장 크다.
3-3. limitation of depth 조건을 만족하는 최적의 트리를 완성하기
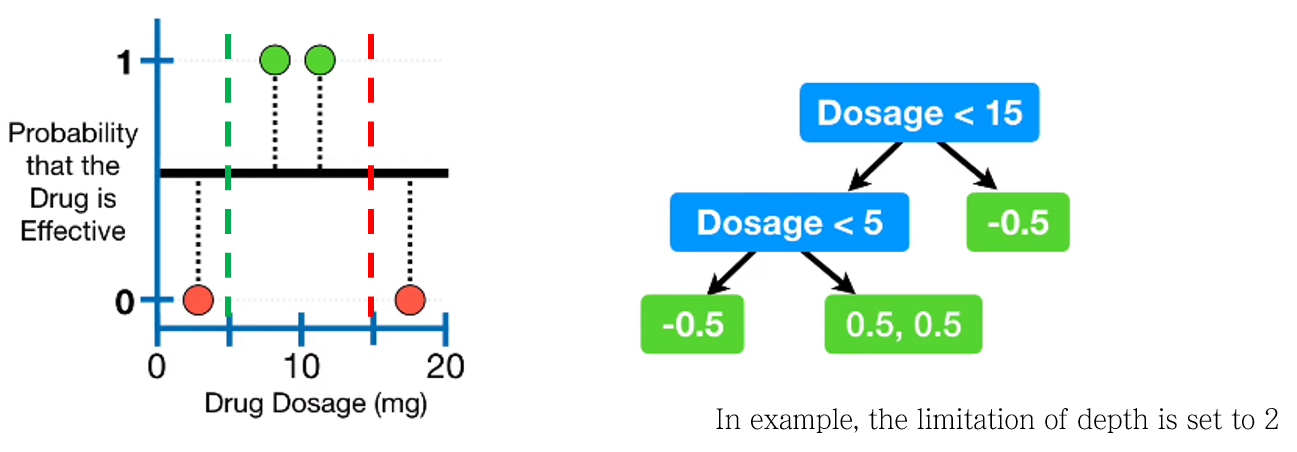
위 예제에서는 limitation of depth=2로 설정되어 있었다.
같은 방법으로 최대 gain 조건을 찾아 분기를 하여 tree를 완성한다.
3-4. Prune
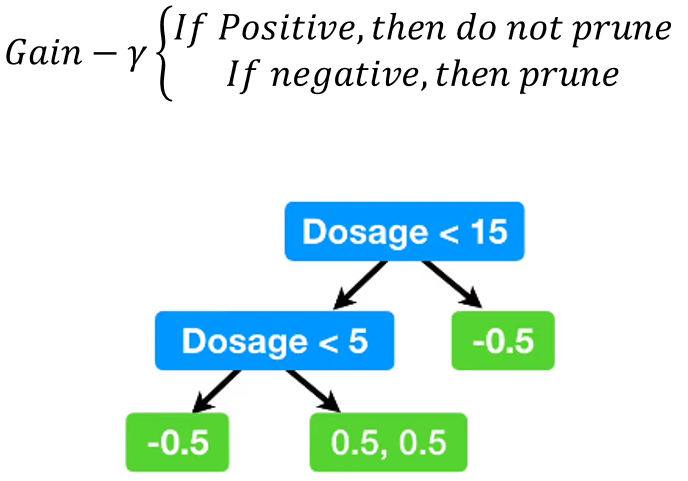
gamma는 미리 정해두는 hyperparameter.
만약 gain - gamma가 negative면 가지치기로 삭제
3-5. Representative value 계산

각 leaf에 대해서 representative value = output value를 계산한다.
4. Predicted probability 계산
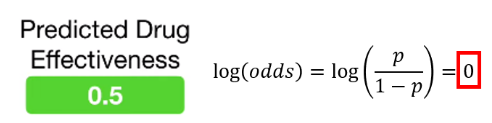
first leaf의 값을 log(odds)로 변환해준다.
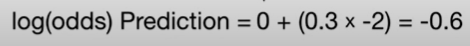
모델의 leaf의 output value에 learning rate를 곱하고 first leaf의 log(odds)값과 더한다.
이 문제에서 learning rate는 0.3이다.
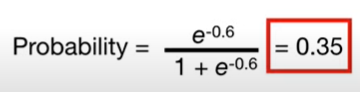
이 값을 logistic function에 넣으면 predicted probability를 구할 수 있다.
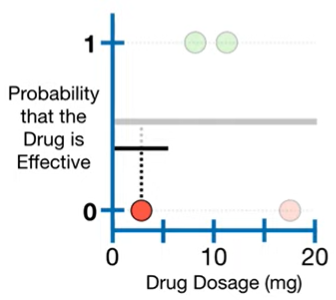
0.35는 첫번째 트리에서 예측한 0.5보다 ground truth 값에 가까워졌다.
모든 output value에 대해서 이 과정을 수행하여 모든 data point에 대한 predicted probability를 구한다.
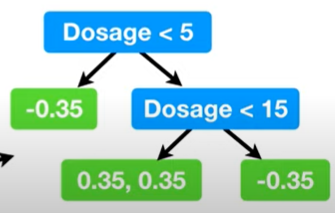
구한 residual로 새로운 tree를 만든다.
5. Repeat 2-4
maximum number of tree에 도달하거나, residual이 지정한 threshold 이하로 떨어질 때까지 반복한다.
6. Test
XGBoost 개념 이해
XGBoost 알고리즘의 개념 이해 조대협 (http://bcho.tistory.com) XGBoost는 Gradient Boosting 알고리즘을 분산환경에서도 실행할 수 있도록 구현해놓은 라이브러리이다. Regression, Classification 문제를 모두 지원
bcho.tistory.com
https://webnautes.tistory.com/1643
XGBoost 개념 정리
XGBoost 관련 개념을 정리한 문서입니다. 논문을 보고 진행했어야 했는데 인터넷 자료를 바탕으로 작성하게 되었네요. 수식은 이해안되는 부분이 아직은 많아서 제외시켰습니다. 추후 논문을 확
webnautes.tistory.com
머신러닝 - 4. 결정 트리(Decision Tree)
결정 트리(Decision Tree, 의사결정트리, 의사결정나무라고도 함)는 분류(Classification)와 회귀(Regression) 모두 가능한 지도 학습 모델 중 하나입니다. 결정 트리는 스무고개 하듯이 예/아니오 질문을 이
bkshin.tistory.com
머신러닝 - 5. 랜덤 포레스트(Random Forest)
이전 포스트에서 결정 트리(Decision Tree)에 대해 알아봤습니다. 랜덤 포레스트를 배우기 위해서는 우선 결정 트리부터 알아야 합니다. 결정 트리에 대해 잘 모른다면 이전 포스트를 먼저 보고 오
bkshin.tistory.com
https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-14-AdaBoost
머신러닝 - 14. 에이다 부스트(AdaBoost)
본 챕터에서는 부스팅 기법 중 가장 기본이 되는 AdaBoost에 대해 알아보겠습니다. 부스팅에 대해서 잘 모르신다면 '머신러닝 - 11. 앙상블 학습 (Ensemble Learning): 배깅(Bagging)과 부스팅(Boosting)'을 참
bkshin.tistory.com
https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-15-Gradient-Boost
머신러닝 - 15. 그레디언트 부스트(Gradient Boost)
앙상블 방법론에는 부스팅과 배깅이 있습니다. (머신러닝 - 11. 앙상블 학습 (Ensemble Learning): 배깅(Bagging)과 부스팅(Boosting)) 배깅의 대표적인 모델은 랜덤 포레스트가 있고, 부스팅의 대표적인 모
bkshin.tistory.com
[ML] XGBoost 개념 이해
Boosting 이란? 여러 개의 약한 Decision Tree를 조합해서 사용하는 Ensemble 기법 중 하나이다. 즉, 약한 예측 모형들의 학습 에러에 가중치를 두고, 순차적으로 다음 학습 모델에 반영하여 강한 예측모
wooono.tistory.com
https://tyami.github.io/machine%20learning/ensemble-7-boosting-XGBoost-classification/
부스팅 앙상블 (Boosting Ensemble) 3-2: XGBoost for Classification
Boosting 모델 중 하나인 XGBoost의 Classification 알고리즘을 정리해봅시다
tyami.github.io
https://www.youtube.com/watch?v=8b1JEDvenQU
Decision Trees Explained — Entropy, Information Gain, Gini Index, CCP Pruning..
Though Decision Trees look simple and intuitive, there is nothing very simple about how the algorithm goes about the process deciding on…
towardsdatascience.com
'DL_general' 카테고리의 다른 글
| 학습 중 GPU를 100% 쓰지 않는 이유, GPU util을 올리려면? (0) | 2023.03.23 |
|---|---|
| localization (0) | 2023.03.15 |
| YOLO (0) | 2023.03.13 |
| cosine similarity (0) | 2023.03.08 |
| auto encoder (0) | 2023.03.07 |



